#10 - Potência
É o quanto de Energia (∆E ou 𝝉) transformada por unidade de tempo.
Ex: Chuveiro , motor de carro, etc.
Quanto mais converter energia em uma quantidade de tempo, mais potente é o motor / maquina .
Dois carros saem da praia em direção a serra (h=600m). Um dos carros realiza a viagem em 1hora, o outro demora 2horas para chegar. Qual dos carros realizou maior trabalho?
Nenhum dos dois. O Trabalho foi exatamente o mesmo. Entretanto, o carro que andou mais rápido desenvolveu uma Potência maior.
A unidade de potência no SI é o watt (W).
Além do watt, usa-se com frequência as unidades:
1kW (1 quilowatt) = 1000W
1MW (1 megawatt) = 1000000W = 1000kW
1cv (1 cavalo-vapor) = 735W
1HP (1 horse-power) = 746W

Vamos considerar um caso particular em que uma força constante 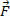 atua num corpo durante um intervalo de tempo Δt, em que o deslocamento é
atua num corpo durante um intervalo de tempo Δt, em que o deslocamento é 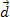 , como mostra a figura acima. A potência média da força nesse intervalo de tempo é:
, como mostra a figura acima. A potência média da força nesse intervalo de tempo é:
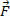 atua num corpo durante um intervalo de tempo Δt, em que o deslocamento é
atua num corpo durante um intervalo de tempo Δt, em que o deslocamento é 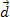 , como mostra a figura acima. A potência média da força nesse intervalo de tempo é:
, como mostra a figura acima. A potência média da força nesse intervalo de tempo é: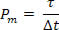
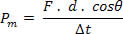
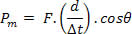
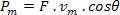
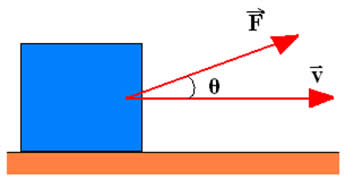
Na fórmula, vm é o módulo da velocidade média. Se usássemos cálculo diferencial, poderíamos mostrar que a fórmula pode ser estendida para valores instantâneos. A figura abaixo nos mostra o instante em que a força forma um ângulo Ө com a velocidade, nesse caso a potência é dada por:
P = F . v . cosӨ
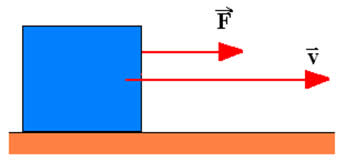
No caso particular em que a força é paralela à velocidade, isto é, Ө = 0° e cos 0º = 1, temos que a potência calculada é:
P = F . v
Rendimento
Em nosso dia a dia é muito comum falarmos em rendimento, seja na escola, no trabalho ou até mesmo quando queremos saber quantos quilômetros um automóvel faz com um litro de combustível. No estudo de Física, a noção de rendimento está ligada à energia e potência.
Todas as vezes que uma máquina realiza um trabalho, parte de sua energia total é dissipada, seja por motivos de falha ou até mesmo devido ao atrito.
Todas as vezes que uma máquina realiza um trabalho, parte de sua energia total é dissipada, seja por motivos de falha ou até mesmo devido ao atrito.
Consideramos então que :
Pt = Pu + Pd
Pt: Potência Total
Pu: Potência Util
Pd: Potência Dissipada
Desse modo, toda máquina possui um rendimento (η), que é o quociente entre a potência útil (ou seja, utilizada na realização da tarefa) e a potência total. Por definição temos:

Por se tratar de um quociente de grandezas de mesma unidade, rendimento é uma grandeza adimensional, ou seja, ele não possui unidade. Rendimento é expresso em porcentagem e ele é sempre menor que um e maior que zero 0< η<1.




Comentários
Postar um comentário